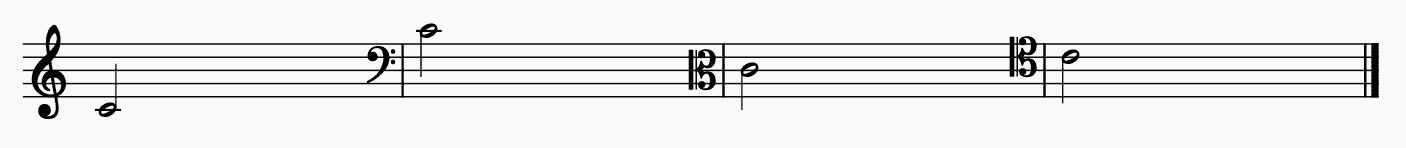Music World

Pitch Names

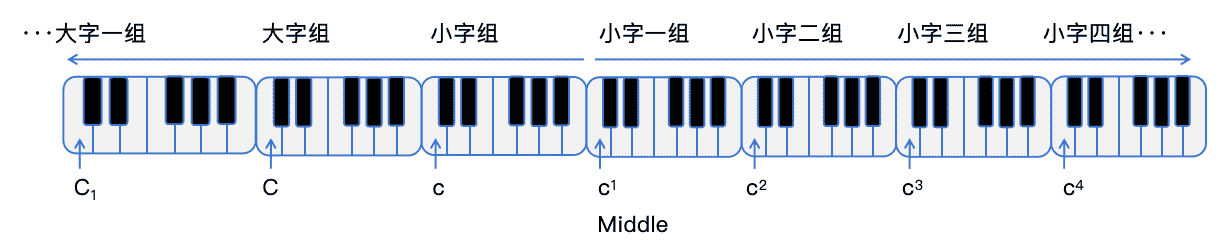
Identifying Middle C Positions in Different Clefs

The Musical Pitch System

The term "Musical Pitch System" can be divided into two parts: "Musical Pitch" and "System".

Music contains not only musical tones but also noise. Do you think noise is unpleasant music while musical tones are pleasant? Actually, their distinction depends on whether the vibration of the sound is regular and whether it has a fixed pitch. Sounds without fixed pitch are collectively called noise, and vice versa. The most common noise instrument is the drum set.

Example: When building a house, do you need many materials and instructions? In the music world, these "bricks" need to have "fixed pitch", such as do, re, mi, fa, sol, la, ti. The 88 keys of the piano are a ready-made, most commonly used set of "brick samples". But there are more "bricks" available in the world than these. The system is the instruction manual for the bricks, organizing the tones, such as according to the major scale (whole-whole-half-whole-whole-whole-half), building something bright and cheerful.

Scale Degree

Basic Scale Degrees (Diatonic): Each independent tone in the musical pitch system is called a scale degree:

Basic Scale Degrees (Diatonic Scale Degrees), Altered Scale Degrees (Chromatic/Altered Scale Degrees).

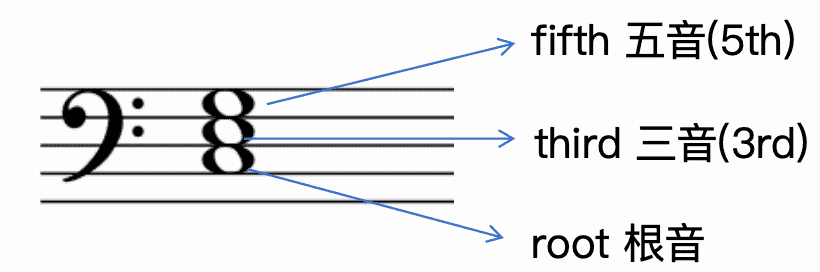
Basic Scale Degrees

Basic Scale Degree	C	D	E	F	G	A	B
Pitch Name	C	D	E	F	G	A	B
Solfeggio	do	re	mi	fa	sol	la	ti
Roman Numeral	I	ii	iii	IV	V	vi	vii
Function Names	Tonic	Supertonic	Mediant	Subdominant	Dominant	Submediant	Leading Tone

Are the function names difficult to remember? Let me help you!

1. Tonic (abbreviation T) should be very familiar to everyone;

2. Supertonic, above the tonic, adding "super" means above the tonic;

3. Mediant, in the middle between the tonic and dominant;

4. Subdominant, below the dominant is subdominant;

5. Dominant (abbreviation D);

6. Submediant;

7. Leading Tone (abbreviation LT).

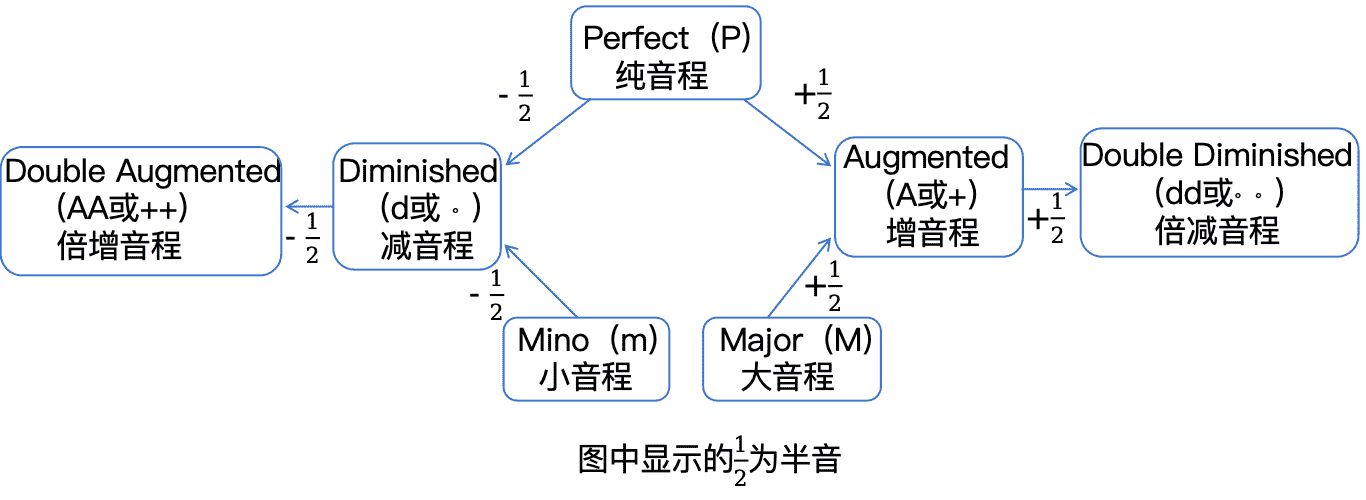
Altered Scale Degrees

Tones raised or lowered based on the basic scale degrees.

Accidental	Description
♯(Sharp)	Raises the basic scale degree by a half step
♭(Flat)	Lowers the basic scale degree by a half step
♮(Natural)	Restores a raised or lowered tone to its original pitch
♭♭(Double Flat)	Lowers the basic scale degree by a whole step
X(Double Sharp)	Raises the basic scale degree by a whole step

Octave and Twelve-Tone Equal Temperament

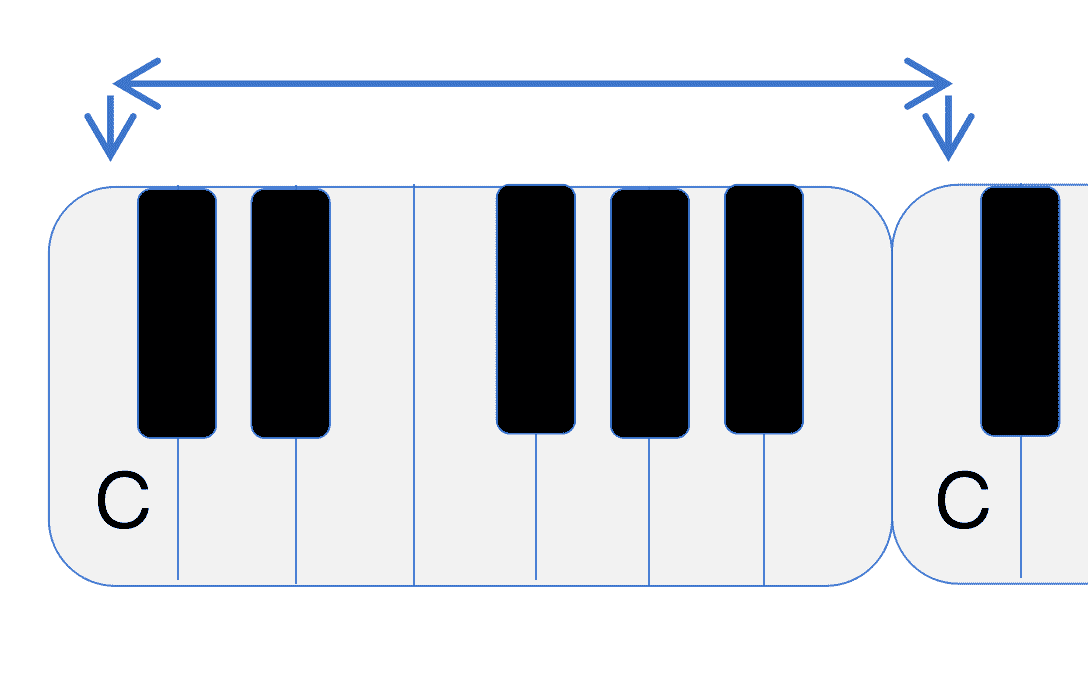
The distance between C in one octave and C in the next octave forms a perfect octave. Dividing the perfect octave into twelve equal parts, with the distance between each part being an equal half step, is called twelve-tone equal temperament.

Enharmonic Notes

Notes that have the same pitch but different meanings and notations are called enharmonic notes.

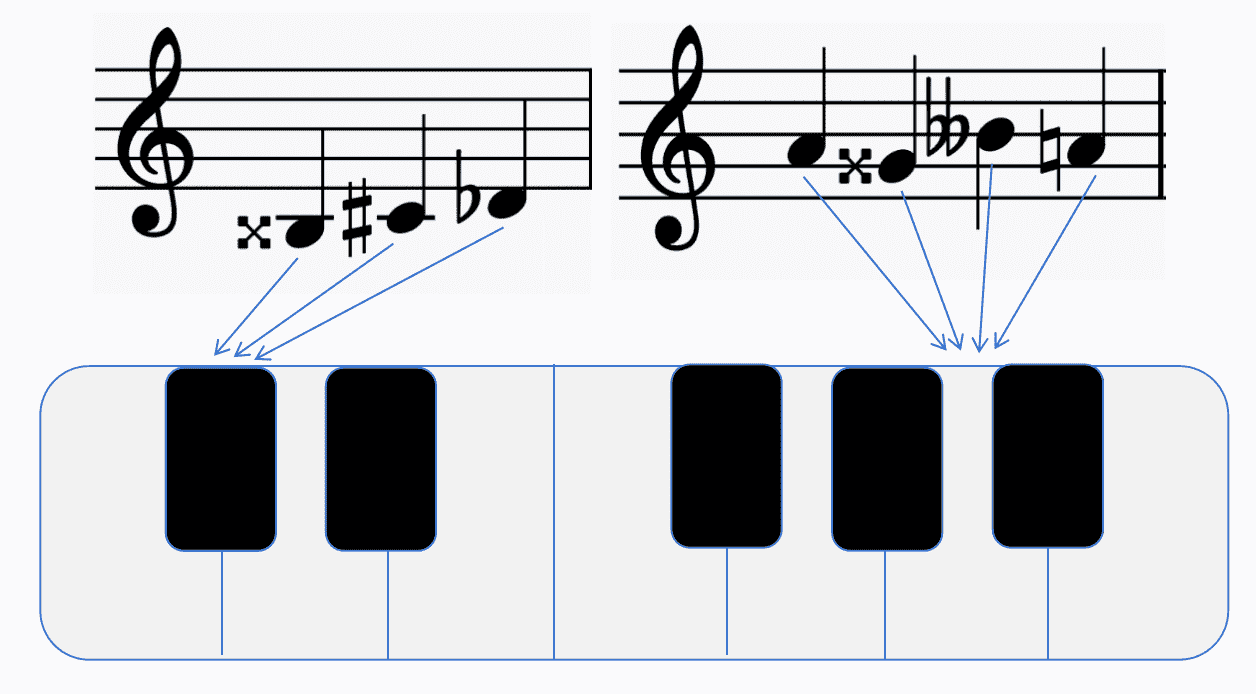
Half Step and Whole Step

Diatonic Half Step, Chromatic Half Step, Diatonic Whole Step, Chromatic Whole Step

Diatonic Half Step: Adjacent different pitch names (e.g., E-F, B-C)

Chromatic Half Step: Same pitch name with accidental (e.g., C-C#, G-Gb)

Diatonic Whole Step: Adjacent different pitch names (e.g., C-D, G-A)

Chromatic Whole Step: Same pitch name with accidental (e.g., Cb-C#, C-CX)

Quick Identification Method:

1. Determine if the distance between two tones is a half step or whole step

2. Are the two tones adjacent after removing accidentals? (e.g., C-D are adjacent, C-C# are not adjacent)

Adjacent - Diatonic; Not adjacent - Chromatic

3. Conclusion: Adjacent tones (half step relationship) - Diatonic Half Step;

Non-adjacent tones (half step relationship) - Chromatic Half Step; Non-adjacent tones (whole step relationship) - Chromatic Whole Step.

Tetrachord:

A tetrachord is a fixed formula of four notes used to construct larger scale systems. It is the "ancestor" of modern scales. In ancient and medieval times, people didn't create songs directly using tones within an octave like we do. They first invented small core groups of four notes.

Tetrachords have their own fixed arrangement patterns, the most classic being: "whole-whole-half" (C-D-E-F)

Two such tetrachords are joined together to form a complete octave scale.

Example: First tetrachord: C-D-E-F (whole-whole-half)

Second tetrachord: G-A-B-C (whole-whole-half)

Combined result: C-D-E-F-G-A-B-C (This is the prototype of what later became the C major scale!)

Dots and Ties: Dotted quarter note; Double dotted quarter note...

Time Signature: ²/₄ time ³/₄ time ⁶/₈ time

Meter, How to Describe Meter?

Meter = _____________________  , _____________________

                    (Simple or Compound)         (Duple or Triple or Quadruple)

Both blanks describe the numerator part of the time signature = ^numerator/_denominator. Is it easy to confuse the numerator and denominator positions?

Memory technique: Mother carrying child

First blank: Simple: numerator is 2 or 3 or 4     Compound: numerator divisible by 3, greater than 3 (not equal to 3)

Example: ²/₄ time ⁴/₃ time  ³/₈ time ⁴/₂ time                  ⁶/₈ time ⁹/₈ time

Second blank: The numerator indicates how many beats per measure. If each measure has two beats = duple; three beats = triple; four beats = quadruple

Look at an example to understand:

Steps: This is 3/8 time signature

1. First look at whether the numerator belongs to simple (1 or 2 or 3 or 4) or compound (divisible by 3, greater than 3) —— Meter: Simple ;

2. Still looking at the numerator: duple (multiple of 2); triple (multiple of 3); quadruple (multiple of 4) —— Meter: Simple ; Triple .

Tuplet Rules: 3 replaces 2; 2,4 replace 3; 5,6,7 replace 4; 9～15 replace 8

(What is this rule used for? Mainly used in rhythmic grouping and when determining time signatures)

Intervals

The distance in pitch between two notes.

Intervals include melodic intervals and harmonic intervals:

To accurately describe an interval, two aspects are needed: number and quality

1. Interval Number

How to calculate:

C-C (same note) = 1 = Unison

C-D (C,D) = 2 = Second

C-E (C,D,E) = 3 = Third

C-G (C,D,E,F,G) = 5 = Fifth

C-C (higher octave) = 8 = Octave

2. Interval Quality

Main types:

Perfect Intervals: Perfect unison, perfect fourth, perfect fifth, perfect octave

Major Intervals: Major second, major third, major sixth, major seventh

Minor Intervals: Minor second, minor third, minor sixth, minor seventh

Augmented and Diminished Intervals: Augmented fourth, diminished fifth

Consonant and Dissonant Harmonic Intervals

Consonant intervals: Major third M3, minor third m3, major sixth M6, minor sixth m6, perfect fourth P4, perfect fifth P5, perfect octave P8. All others are dissonant intervals.

Interval classification table:

Interval Degree	Interval Name	Number of Half Steps	Interval Examples (Basic Scale Degrees)
Unison	Perfect Unison P1	0	1-1, 2-2, 3-3, 4-4, 5-5, 6-6, 7-7
Second	Minor Second m2	½	3-4, 7-1
	Major Second M2	1	1-2, 2-3, 4-5, 5-6, 6-7
Third	Minor Third m3	1½	2-4, 3-5, 6-1, 7-2
	Major Third M3	2	1-3, 4-6, 5-7
Fourth	Perfect Fourth P4	2½	1-4, 2-5, 3-6, 5-1, 6-2, 7-3
	Augmented Fourth Tritone	3	4-7
Fifth	Diminished Fifth Tritone	3	7-4
	Perfect Fifth P5	3½	1-5, 2-6, 3-7, 4-1, 5-2, 6-3
Sixth	Minor Sixth m6	4	3-1, 6-4, 7-5
	Major Sixth M6	4½	1-6, 2-7, 4-2, 5-3
Seventh	Minor Seventh m7	5	2-1, 3-2, 5-4, 6-5, 7-6
	Major Seventh M7	5½	1-7, 4-3
Octave	Perfect Octave P8	6	1-1, 2-2, 3-3, 4-4, 5-5, 6-6, 7-7

Inversion of Intervals

Unison inverts to octave; second inverts to seventh; third inverts to sixth; fourth inverts to fifth; fifth inverts to fourth; sixth inverts to third; seventh inverts to second; octave inverts to unison. The sum of the degrees of an interval and its inversion is nine.

Perfect intervals invert to perfect intervals; major intervals invert to minor intervals; augmented intervals invert to diminished intervals; doubly augmented intervals invert to doubly diminished intervals, and vice versa.

Enharmonic Intervals

Two intervals that sound the same but have different meanings and notations.

1. Enharmonic intervals with same degree and name

2. Enharmonic intervals with different degrees and names

Triads:

Root Position Triads

1. Root Position Major Triad

Root to third: major third M3, third to fifth: minor third m3, root to fifth: perfect fifth P5, marked as M.

2. Root Position Minor Triad

Root to third: minor third m3, third to fifth: major third M3, root to fifth: perfect fifth P5, marked as m.

3. Root Position Augmented Triad

Root to third: major third M3, third to fifth: major third M3, root to fifth: augmented fifth A5, marked as A or +.

4. Root Position Diminished Triad

Root to third: minor third m3, third to fifth: minor third m3, root to fifth: diminished fifth d5, marked as d or °.

Root Position Seventh Chords

1. Root Position Dominant Seventh Chord

A minor third chord stacked on the fifth of a root position major triad, marked as Mm7.

2. Root Position Major Seventh Chord

A major third chord stacked on the fifth of a root position major triad, marked as MM7 or M7.

3. Root Position Minor Seventh Chord

A major third chord stacked on the fifth of a root position minor triad, marked as m7.

4. Root Position Half-Diminished Seventh Chord

A major third chord stacked on the fifth of a root position diminished triad, marked as dm7 or ø7.

5. Root Position Diminished Seventh Chord

A minor third chord stacked on the fifth of a root position diminished triad, marked as dd7 or °7.

Triad Inversions

A chord with a bass note other than the root is called an inverted chord.

1. Root position, first inversion 6, second inversion 64.

2. Chord notation with letters (called slash chord notation), such as (C / E) means: C chord with E as the lowest note (bass note), the middle slash is generally called slash.

3. Chord notation with Roman numerals, such as (C: I / 3rd) means: I chord with the third as the lowest note; such as (G: ii / 5th) means: ii chord with the fifth as the lowest note.

[Are the root and bass the same? No, the root is the fundamental note of the chord, such as the C chord regardless of inversion, the root is do, the G chord root is sol; the bass may be the root or an inversion, it just refers to the "lowest position" note of this chord.]

Seventh Chord Inversions

Key Signatures

Roman numeral chord notation:

C: I ii iii IV V vi vii° I

Did you notice the uppercase and lowercase Roman numerals? When to use uppercase and lowercase? Major triads uppercase, minor triads lowercase.

Major Key Signatures:

How to identify key signatures?

· Sharps: Look at the last sharp, go up a half step to get the key (e.g., 4#, 1#, 5# — last is 5# — up a half step — A major.)

· Flats: Look at the second to last flat (e.g., 7b, 3b, 6b, 2b — second to last — A♭ major)

Natural Major: 1 2 3 4 5 6 7 1

Natural Minor: 6 7 1 2 3 4 5 6

Harmonic Minor: 6 7 1 2 3 4 #5 6 [Raises the VII scale degree in natural minor]

Harmonic Major: 6 7 1 2 3 4 ♭5 6 [Lowers the VII scale degree in natural minor]

Melodic Minor: Ascending 6-7-1-2-3-#4-#5-6 → Descending 6-7-1-2-3-♮4-♮5-6

[Raises the VI and VII scale degrees in ascending, natural in descending]

Melodic Major: Ascending 6-7-1-2-3-4-5-6 → Descending 6-7-1-2-3-♭4-♭5-6

[Natural in ascending, lowers VI and VII scale degrees in descending]

Parallel Minor: e.g., B♭ major's parallel minor is B♭ minor

Relative Minor: e.g., A major's relative minor is F♯ minor [A minor third below the major key, or a minor third above the minor key]

Resolution of Unstable Intervals and Dissonant Chords

The stability and instability of intervals, consonance and dissonance, have completely different meanings.

The stability of intervals is based on the key - intervals formed by scale degrees I, III, V are stable intervals. Intervals containing II, IV, VI, VII scale degrees are unstable intervals.

The consonance of intervals is based on the sound itself:

1. Perfectly consonant intervals: Perfect unison; perfect octave.

2. Completely consonant intervals: Perfect fourth; perfect fifth.

3. Imperfectly consonant intervals: Major third; minor third; major sixth; minor sixth.

4. Dissonant intervals: ① Extremely dissonant: Minor second; major seventh. ② Dissonant: Minor seventh; major second; augmented and diminished intervals.

Resolving Unstable Intervals

1. Stable scale degrees: I, III, V (stability order: I > V > III), they are the pillars of tonality, the ultimate goal of resolution.

2. Unstable scale degrees: II, IV, VI, VII. They have strong tendencies and need to move by step (ascending or descending second) to the nearest stable scale degree.

I. Resolving Unstable Intervals with Known Key

This is knowing where "home" (tonic) is, all tones move toward "home".

Example: C major

Stable scale degrees: C (I) E (III) G (V)

Unstable scale degrees and their tendencies:

· D (II) — Which stable scale degree is closest to II? — C (I) and E (III) [Both can be chosen, but stability-wise I > III]

· F (IV) — Which stable scale degree is closest to IV? — E (III)

· A (VI) — Which stable scale degree is closest to VI? — G (V)

· B (VII) — Which stable scale degree is closest to VII? — C (I)

Example 1: Resolving a melodic fragment containing unstable intervals

Suppose we have a melody (C major)

Its ending stops on D (II), an unstable tone.

1. D (II) — Which stable scale degree is closest to II? — C (I) and E (III)

2. Since we seek a sense of conclusion at the ending, choose I (descending major second)

Example 2: Resolving a chord containing unstable intervals

Suppose we have a G7 chord in C major [G (V) B (VII) D (II) F (IV)] - unstable chord

1. First identify which of these four tones are stable and unstable — Result: B (VII) D (II) F (IV) are all unstable.

2. D (II) — C (I) and E (III) [Both can be chosen, but stability-wise I > III]

F (IV) — Descending half step — E (III)

B (VII) — Ascending half step — C (I)

II. Resolving Dissonant Chords with Unknown Key

Since the key is unknown, we don't know if they are stable scale degrees, but we can look at the chord vertically. For example, if you see a chord that may contain an augmented fourth, then you need to resolve it, with the two notes of the augmented fourth moving by step to resolve.

Secondary Chords: Secondary Dominant, Secondary Dominant Series, Secondary Subdominant Series

1. Definition: Tonicization is embedding harmonic progressions from other keys within the original key's harmonic progression, creating a temporary sense of leaving the main key.

2. Characteristics: Appearance of temporary accidentals that are non-chord tones; vertically stacked thirds forming chords not in the original key's natural tone system.

3. Categories: Secondary dominant series chords, secondary dominant series chords, secondary subdominant series chords, secondary leading-tone series chords.

Analysis of Secondary Chord Notation Format:

x / y (x: Roman numeral of what degree in the secondary key, inversion must be written; y: Roman numeral degree of the temporary tonic chord in the original key, also called tonicization. The y on the right must be a major or minor triad, cannot be augmented or diminished triad. For example, V/vi means: the V chord in the key where vi is the temporary tonic chord.

[Simply put: Read from left to right, the V chord in the original key on the VI degree, is the root of the new chord. English is also read from left to right, read as: "five of six"]

[Tip: Tonicization: Temporary, local key change that doesn't alter the overall key. Modulation: Complete key change, establishing and maintaining a new key.]

I. Secondary Dominant Series: Secondary Dominant (V/V), Secondary Leading-tone Chord (vii°/V)

Secondary Dominant (V/V):

The secondary dominant is the dominant of the dominant chord, a dominant chord constructed with the diatonic dominant chord as the "temporary tonic chord". For the main tonic chord, it is the secondary dominant chord. [The temporary tonic chord must be a major or minor triad, therefore the VII degree in major keys cannot be a temporary tonic chord because the VII degree in major is a diminished triad.]

Just as the dominant chord resolves to the tonic chord, the secondary dominant chord also resolves to its temporary tonic chord.

Construction of Secondary Dominant (V/V):

The secondary dominant is a major-minor seventh chord constructed on the II scale degree (from bottom up, major-minor-minor structure). In major keys, its characteristic tone is the raised IV scale degree. In minor keys, its characteristic tones are the raised IV and VI scale degrees.

II. Concept and Usage of Secondary Dominant Series Chords:

The difference between secondary dominant series chords and secondary dominant series chords is that secondary dominant series chords are either V/V or vii°/V, both sides are dominant function. Secondary dominant series chords are those other than the dominant chord, such as V/II, V/III, V/IV, V/VI.

The construction method is the same, read from left to right, V/II: The II degree tone on the original key's V degree is the root, then construct upward from there.

III. Concept of Secondary Subdominant Series:

The previous categories were either secondary dominant series or secondary dominant series, both related to dominant function. The secondary subdominant series doesn't revolve around dominant, for example: IV/IV, ii/IV, IV/II.